在抗体与抗原设计优化以及抗体亲和力成熟模拟中,精确高效的计算蛋白质-蛋白质结合亲和力是计算机建模的关键步骤。本研究综合比较了抗体/抗原(Ab/Ag)结合亲和力的三种方法:(i)基于平衡分子动力学 (MD)模拟的Ab/Ag复合物物理分离方法;(ii) 一组应用于同源建模软件生成的结构集合函数;(iii) 基于分子力学-广义Born表面积(MM-GBSA)能量分解的计算方法。用于分析两个抗体(Ab)与HIV 病毒gp120蛋白形成的复合物,其中49个抗体突变,均显示中等准确性,Pearson相关系数约为0.6,且计算成本最高的MD模拟方法并未达到理想的预期效果,说明计算值和实验值存在一定偏差,仍有局限性。在每个方法中,作者检查了独立计算重复的数量,即建模结构或重新初始化的 MD 模拟对预测准确性的影响。作者建议使用大约 10 个建模结构进行评分方法,使用大约 5 个模拟重复进行 MD 模拟,作为获得合理收敛的经验法则。
【引言】
在计算抗体设计中,期望通过优化抗体序列来增强其与抗原的结合亲和力,同时需兼顾其他生物学因素,例如溶解性和避免自身免疫反应。在计算疫苗设计中,优化的目标是开发与特定胚系前体具有高亲和力的抗原,引起机体持久的免疫反应。由于蛋白质序列变异的多样性和复杂性,获得快速计算抗体/抗原(Ab/Ag)结合自由能(bFE)至关重要。
本研究报告了对几种计算 bFE 的方法的比较结果,这些方法的计算成本和准确性各不相同。首先是基于物理的方法,依赖于全原子经典分子动力学(MD)模拟生成显式溶剂中的Ab/Ag结构的热力学集合。优点是唯一的假设是所选的经典势能函数提供了固有量子力学溶剂化蛋白质复合物的能量的准确近似值。然而,此方法需要很长的模拟时间,通常为数百纳秒到微秒,对应于数十亿到数万亿次能量梯度评估,尚未在实际抗体或抗原设计中常规使用。但是使用图形处理器单元(GPU)的模拟软件和基于扩展统计机械集合的理论算法不断进步,使基于 MD 的方法更具竞争力。
更加实证的方法是使用评分函数直接近似bFE。从技术上讲,这种方法只需要单一结构,可以从蛋白质数据库 (PDB)、同源或从头开始建模中获得。然而,由于蛋白质在溶液中是灵活的,因此结合反应中的结合态、未结合态甚至过渡态都由许多不同的结构或微观状态和宏观态组成,这些结构或微观状态和宏观态有助于结合。因此,单一结构方法必须隐含地表示潜在的异质结构集合,这可能会限制其预测准确性。
提高单结构方法准确性的一个想法是对多个结构进行评分。然而,通常不清楚应该使用多少结构来平衡良好的速度与精度。例如,同源建模程序生成的不同模型在结构上可能相似。此外,复杂的结构建模算法可能需要几分钟到几小时,从而限制了高通量应用。当使用基于热力学集合的方法(如 MD)时,由于蛋白质的空间构象的复杂性,探索蛋白质的三维结构可能非常缓慢,因此从不同的初始结构或不同的速度实现开始重复模拟也可能是有利的。本研究除了评估计算 Ab/Ag 结合亲和力的不同方法外,作者还研究了结构数量对计算亲和力准确性的影响。单结构评分方法以及 MD 模拟分别使用多个结构或模拟重复进行测试。
【内容介绍】
1. 选择HIV包膜糖蛋白 gp120与VRC01广泛中和抗体结合亲和力作为实验数据集
首先根据Clark等人的研究提供的结合亲和力实验数据集,他们使用了与抗体 VRC01、VRC03 或 VRC-PG04 结合的表面稳定核心抗原(RSC3),本研究仅考虑VRC01,包括未突变体和29个单点丙氨酸突变体。使用PDB结构3NGB作为模板,由于PDB中没有RSC3的结构,所以抗原采用93TH057,根据Zhou等人对93TH057与VRC01之间的研究,获得了19组数据。从两组研究中共获得49种实验结合亲和力数据(如表1)。
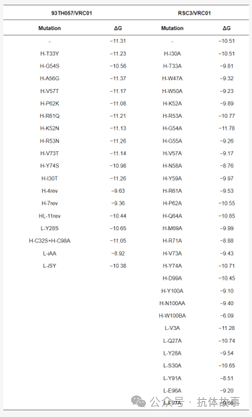
表1:本研究中使用的 49 种实验性结合亲和力的数据集(能量以 kcal/mol 为单位表示)前缀 H- 或 L- 分别表示突变是针对重链还是轻链;突变体末尾的字母对对应于相对于种系序列的残基插入代码,后跟突变后残基的字母代码。它们是:H-4rev—A56G、V57T、P62K、V73T(重链);H-7rev—T33Y、G55S、A56G、V57T、P62K、V73T、Y74S(重链);HL-11rev 链条:I30T、K52N、R53N、G54S、A56G、V57T、R61Q、P62K、V73T、Y74S(重链)、Y28S(轻链)。
2. 通过PMF 计算结合自由能
传统的分子动力学模拟是基于经典的统计热力学,计算蛋白质-配体之间结合的自由能,本研究采用一种新型薄柔溶剂层,替代了本体溶剂,应用于计算流感血凝素(HA)抗原和抗HA抗体的平均力(PMF)时,计算结果和实验数据取得良好的一致性。在计算gp120与VRC01结合亲和力时,也采用了这种方法。本研究仅保留了抗体的可变段和gp120抗原的部分残基,使用 Modeller构建了 gp120 的环残基 318-323 的缺失坐标,并使用 CHARMM 通过将侧链截断来形成丙氨酸的残基突变。使用ProPka3程序检查模拟结构,认为质子化状态对结合亲和力计算结果影响不大。使用CHARMM36能量函数和PME程序OpenMM进行MD模拟。为了计算抗体与抗原分离的PMF,本研究使用了平底约束方法,并施加了额外的约束来限制抗体的平移和旋转(如图1)。
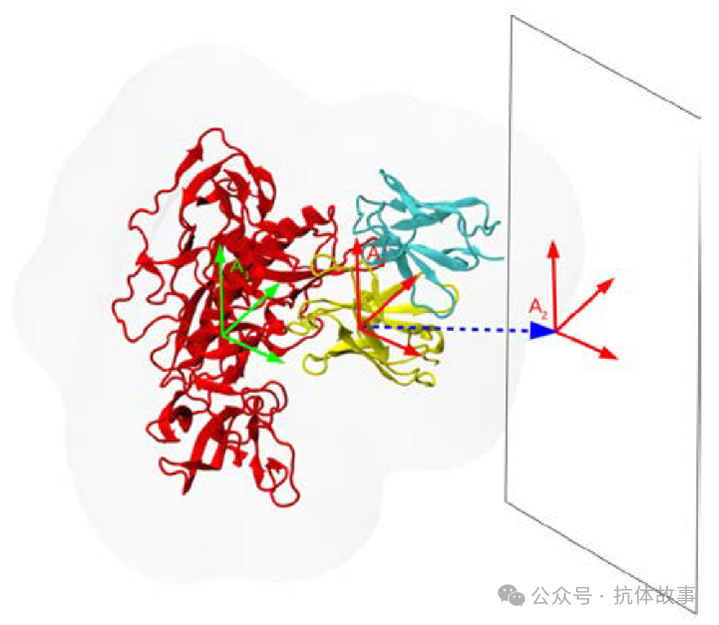
图1:用于计算 Ab 与 HIV gp120 Ag 解离的 PMF 的程序示意图。从结合的 Ab/Ag 复合物开始,Ab 沿着指向 Ab COM 的载体(蓝色虚线)从 Ag(红色)移位,该载体指向 Ab 之间的分离方向(重链为黄色, 青色轻链)。
PMF模拟结果如图2和图3,可以看到模拟和实验之间的总体相关性相当适中, rp = 0.49 和 RMSE = 2.09 kcal/mol 。这种差异比 Clark 等人使用自由能微扰 (FEP) 结合溶质回火(REST)的复制品交换获得的差异更大,即 rp = 0.71 和 RMSE = 0.64 kcal/mol。但本研究的结果因突变类型而异,极性和非极性残基的突变,rp = 0.56 和 RMSE = 1.44 kcal/mol;带电残基突变, rp = 0.66 和 RMSE = 3.5 kcal/mol,前者相关性和RMSE更好,这表明模拟通常反映了自由能变化的方向,但高估了大小,这可以用突变残基及其环境的不完全结构弛豫来解释。此外,本研究采用针对丙氨酸的突变,丙氨酸具有非极性侧链。基于静电考虑,作者预计非极性残基的突变需要较少的结构松弛,而涉及带电残基的突变需要更多结构松弛。
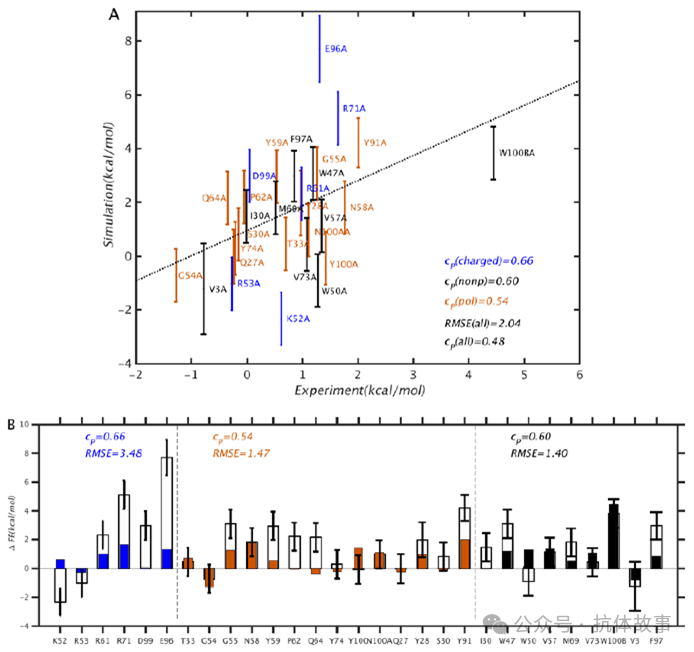
图2:根据PMF 模拟结果和实验计算的结合自由能 (bFE) 差异之间的比较。在 (A) 中,对应于带电、极性和非极性残基的突变分别以蓝色、棕色和黑色着色,虚线对应于 y = x。在 (B) 中,分别比较了突变数据。残基 V3、Q27、Y28、S30、Y91、E96 和 F97 在 Ab 轻链中,其余残基在重链中。
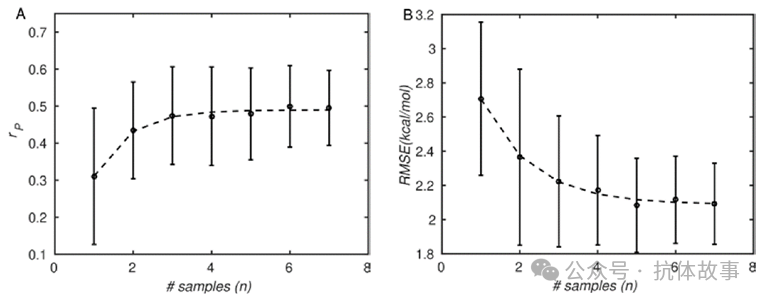
图3:PMF 仿真结果与实验之间的一致性随着仿真重复次数的增加而提高.(A):皮尔逊相关系数 (rP);(B):均方根误差 (RMSE)。
一个样本的Pearson相关系数约0.3 ± 0.2,三个样本的情况下,Pearson 相关系数已经在 0.45 ± 0.15,直到七个样本的约 0.5 ± 0.1,这表明重复模拟次数能够提高相关性。相应地,RMSE从约 2.75 kcal/mol 降低到约 2.09 kcal/mol。这说明多个模拟重复可以提高准确度和精密度。作者建议进行 5次模拟重复。但是,即使在这里进行了 7 次 PMF 仿真重复,Pearson 相关性和 RMSE 的不确定性仍然相当高。作者提醒本研究的PMF方法不使用增强的采样方法,如复制品交换或回火。使用这些方法可能会减少收敛所需的样本数量,因为它们是专门为加速对构型空间的探索而设计的,因此增加了单个仿真轨迹内的去相关。
3.使用不同的快速评分函数计算蛋白质-蛋白质结合自由能
鉴于上述PMF模拟的计算成本高且结果质量一般,考虑评分函数是否可以提供类似的准确度,对于降低计算成本很有意义。
首先使用同源建模程序Modeller和Rosetta 为每个复合物生成一组模型,然后应用多个评分函数进行计算,包括5种对接的评分函数ZRANK 、ZRANK2、PyDock、ATTRACT和FireDock,8种基于统计学原理的统计势评分函数DOPE、DOPE-HR、RF_HA_SRS、RF_CB_SRS_OD、ipot_aace167、ipot_aace18、ipot_aace20和ipot_rrce20,2种能量函数Rosetta和FoldX和最终评分函数Prodigy,将所有函数计算结果进行平均,计算结合亲和力,比较函数对于模型变化的敏感性和预估获得可靠数据所需模型的数量。
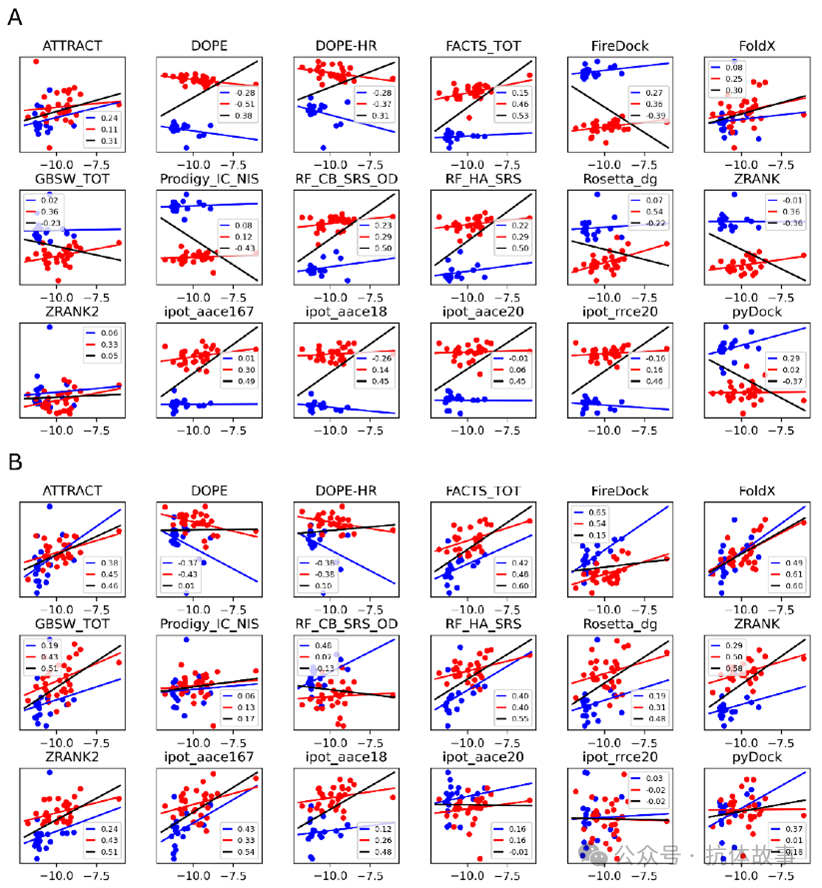
图4:使用 18 个快速评分函数测定实验和计算的结合亲和力之间的相关性。(A):结构是使用 Modeller 生成的;(B):结构是使用Rosetta 生成的。与 RSC3 抗原的复合物的数据以红色表示,与 93TH057 抗原的复合物的数据以蓝色表示,黑线对应于整体相关性。图例中的数字是Pearson 相关系数。
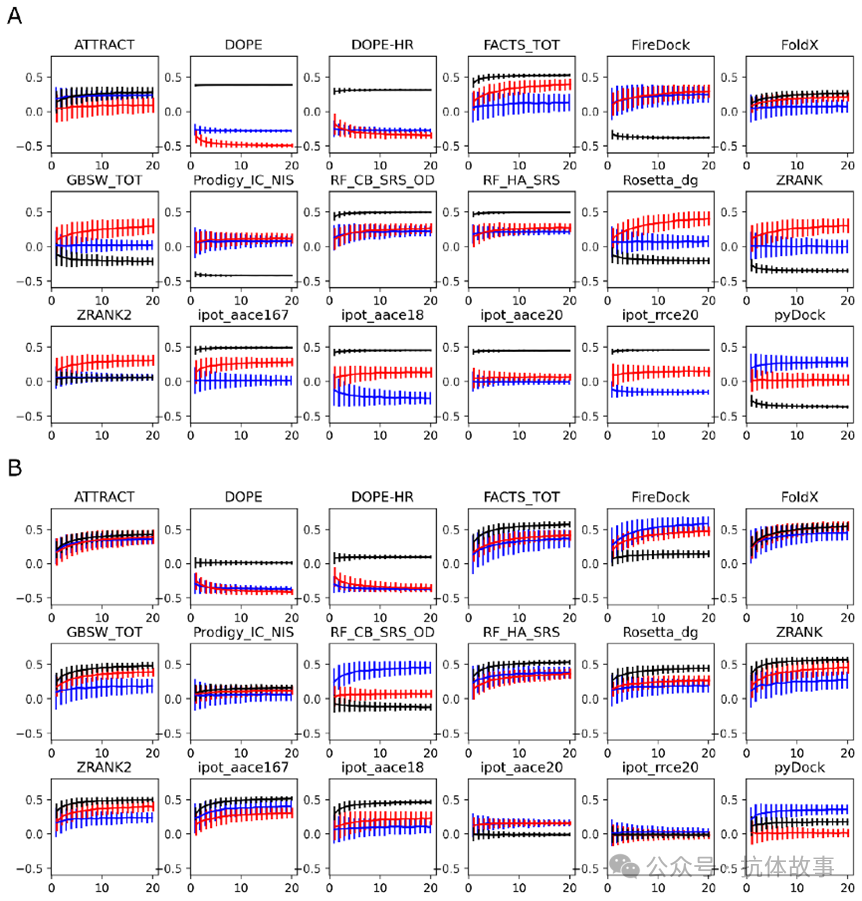
图5:实验和计算的结合亲和力之间的Pearson 相关系数与每个评分函数的平均值中使用的模型数量的收敛性。(A):结构是使用 Modeller 生成的;(B):结构是使用 Rosetta 生成的。与 RSC3 抗原的复合物的数据以红色表示,与 93TH057 抗原的复合物的数据以蓝色表示,黑线对应于整体相关性。
对于几个评分函数,相关系数达到0.6。对于表现最佳的评分函数,例如 ATTRACT 或 FoldX,相关系数与结构数量的增加更为明显。似乎需要大约10个结构才能达到20个结构集合平均值获得的90%的相关性,即使是20个结构也无法完全达到稳定状态。
4.隐式溶剂化模型计算蛋白质-蛋白质结合自由能
采用MM-GBSA方法计算,它将总能量分解为几个部分:分子力学(MM)能量、广义Born(GB)极性溶剂化贡献,以及与溶剂可及表面积(SASA)成正比的非极性溶剂化项。并测试了两个GB模型GBSW和CHARMM。
公式为: ΔG = ΔE毫米+ ΔG国标+ γΔSASA
(E毫米是使用经验势能函数(此处为CHARMM36能函数)获得的经典能量,其中包括键合能项、范德华和静电相互作用 G国标是广义的 Born 溶剂化自由能,γ 是经验表面张力系数。)
随后,为了提高实验与 MM-GBSA 隐含溶剂结果之间的一致性,作者优化了各个能量项的系数,
将 ΔG 写为: ΔG = aΔE电子+ bΔEVDW+ cΔG国标+ dΔSASA + e
(a-e 是适合实验结合亲和力的自由参数)
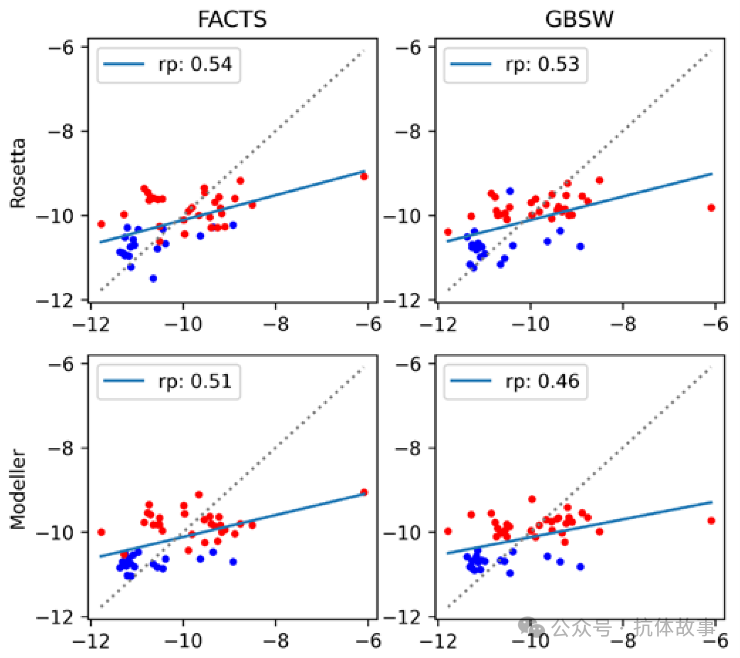
图6:使用重构的 MM-GBSA 模型进行实验和计算的结合亲和力之间的相关性
表2:由 GBSW 和 FACTS 隐式溶剂在 Rosetta 和 Modeller 结构上生成的四个模型的拟合参数(方程 (2))和回归统计量。Pearson 相关系数的统计不确定性约为 0.02。(能量以 kcal/mol 为单位表示)
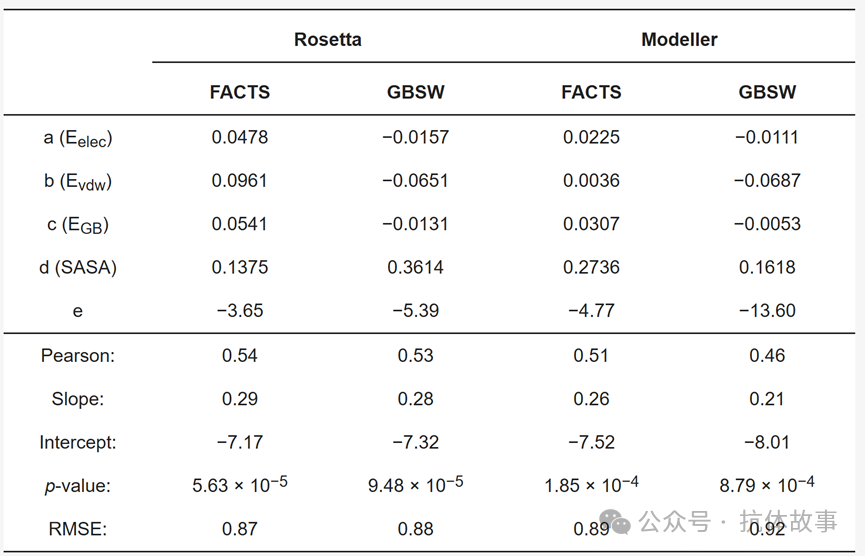
优化系数能够提高计算结果与实验数据的一致性,优化后的模型,如应用于Rosetta结构的refit FACTS模型,其相关系数(rp = 0.54)与最佳评分函数相当,表明优化过程有效。均方根误差(RMSE)在0.88-0.92 kcal/mol范围内。但仍存在一些问题,GBSW模型的系数出现了负值,这与实际实验值有很大的偏差。对于Modeller生成的结构,范德华(vdW)值降低,而对于Rosetta生成的结构,vdW值却更高,这表明了模型有时会偏离实际实验值。
【小结】
高效准确地计算蛋白质间的结合自由能 (bFE) 是抗体 (Ab) 和抗原(Ag) 设计的重要组成部分。在本研究中,我们比较了几种计算 bFE 的方法,力求在速度和准确性之间找到最佳折衷方案,以用于亲和力成熟模拟以及抗体和抗原设计。
当一小组丙氨酸突变时,PMF模拟和评分函数能够获得近似的较为准确的结果,对于同一数据集,FMP模拟能够获得精度更高的数据,这表明 FEP 可能是相对简单的结构突变的首选方法。另一方面,在涉及蛋白质骨架拓扑变化的情况(例如删除和插入一个或多个残基)中,PMF方法仍然是首选。作者提醒,当前的简单丙氨酸扫描突变测试集可能无法代表该方法在应用于如此复杂的突变时的准确性。
作者还考虑了独立结构的数量(对于快速评分方法)或独立模拟重复的数量(对于PMF模拟)对预测精度的影响。观察到精度随着结构数量的增加而增加,但增加的速度取决于所用的方法。根据目前结果,建议对于评分函数方法使用大约10个结构,对于基于MD的方法使用大约5个模拟重复,但确切的数量将取决于方法细节。
为进一步提高准确性,作者考虑了可通过经验调整的结合亲和力方法,并使用一些预先存在的结合数据进行训练。具体来说,使用了MM-GBSA模型中的能量分解形式,以优化不同能量项对bFE的附加贡献。尽管这种方法与实验结合自由能差异的一致性最好,但它的缺点是需要“训练”集,因此不是先验预测。此外,由于允许能量贡献系数任意变化以获得最佳拟合,其中一些变为负值,清楚地表明了非物理行为。尽管如此,少量的实验结合数据用于模型训练,这种半经验方法也是合理的。拟合过程的进一步扩展可以超越线性回归,扩展到更复杂的机器学习方法。
鉴于作者研究报告的准确性有限,使用本文描述的结合亲和力方法优化很可能不会导致抗体亲和力提高。然而,创建大且多样化序列集的优化策略,尽管相关性相当小,仍然可以发现高度优化的抗体。
【原文出处】 Conti S, Lau EY, Ovchinnikov V. On the Rapid Calculation of Binding Affinities for Antigen and Antibody Design and Affinity Maturation Simulations. Antibodies, 2022, 11(3):51. 原文链接:https://doi.org/10.3390/antib11030051 指导教师:王战辉